A math question that I can't quite get my head around....

[naaman]

I swear! The things that go through my head when I'm bored....:redface:

Okay so here it is:

If there is a given likelyhood of something occuring, we can represent that with a percentage. Such as 30% likely.

Now, if the likelihood doubles, it should become 60% likely, right?

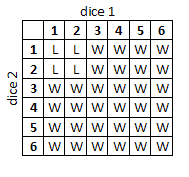
But, what if the likelihood doubled again? For example, you roll a die and you are looking for it to come up as a 3 or higher (66.67% chance). Now, if you roll two dice and need at least one (both are not necessary) to come up three or better, the likelihood is doubled, but what percentage is it that one or the other will come up three or better? It's obviously not 133%.

The only thing I could think of would be to cut the likelihood of failure in half. So for example, on a single die you have a 33.3% chance to fail, while the chances of both dice failing is only 16.67%. But then, that's not really "doubling" the chance for success, since by that method your chances for success are 83.3%, which is not twice as much as 66.67%.

Since the outcome of the first die has no impact on the outcome of the second die, the odds should be doubled, but I can't figure out how to represent that with a percentage.

So what is the answer? I'm stumped.

 

[RSO 34]

You still have a 66.67% chance of rolling one die with a 3 or higher. One die is a 4/6 chance and getting one out of two dice to be 3 or higher is an 8/12 chance - still 66.7%.

 

[Vega$ NSX]

You still have a 66.67% chance of rolling one die with a 3 or higher.

Yup what he said. The odds of rolling a 3 or higher is the same 66.67%. It doesn't matter if you rolled two dice at the same time or the same die twice in a row. Each roll has a 66.67% chance of landing on a 3 or higher.

I think the problem that you are running in to is that you are mistakenly thinking that your odds double if you roll two dice or roll the same die twice. The odds do not improve, they stay the same. Think of it this way. If you roll a die once, you have a 4 in 6 chance of rolling a 3 or higher. That equal 66.67%. If you roll a die twice, or two dice, you need to count the total winning possibilities divided by the total opportunities; which in this case is 8 in 12 chance of rolling a 3 or higher. However, that percentage stays the same at 66.67%. If you roll three dice or three times, then you have 12 winning possibilities with 18 total possibilities; again 66.67%.

 

[White92]

I think there is a 167% chance that I'm confused by this thread.

 

[naaman]

Are you absolutely sure? I mean... is there some kind of formula that applies to probabilites like this?

If the odds are the same regardless of how many dice your roll (or how many times you roll the same die) then there is no statistical benefit to "trying again for free," right?

Okay, re-reading my first post, there is something that may make it make sense.

With the requirement that any one die come up a 3 or better, your chance of failure on a single die is 33.3%. Now, if you roll two dice, the only way you could fail would be if both dice came up as a 1 or 2. The odds of one die showing up as 1 or 2 are 33.3%. But the odds of both dice (as opposed to one or the other) coming up as 1 or 2 are only 16.67%, right? So the chance of failure diminishes, does it not? Which translates to the odds of success increasing... right...?

 

[Ojas]

I respectfully disagree with RSO and Vega$ NSX. With two dice, your chances are 8/9.

Compared to rolling one die, you chances must improve with two since you can now fall back on the second die if the first one rolls 1 or 2. Remember, the criteria for success is that at least one, not necessarily both, must roll 3 or higher. Look at it this way:

Let's call the dice D1 and D2 and let's just look at D1 first. You have a 2/3 chance of success based only on D1. That means there's a 1/3 chance where you'll want to check D2, which itself has a 2/3 chance of success.

2/3 + 1/3 * 2/3 = 8/9

If you don't believe your chances improve with two dice, imagine rolling 3, 4, 100, 1000, or a million. You can see your chances of success approach 100%, but never reach it (there's always the chance that all million dice will roll either 1 or 2).

 

[whatisreal7]

You have to divide 132% by 2!, or 2 factorial, or 2x1, or 2. That gives you 66% again.

The easiest way to look at it is this:
Two die has 12 faces. There are 8 total numbers on the two die that are greater than 3. That means each time you roll the dice, there is 8/12 chance you will get a number higher than 3.

 

[whatisreal7]

I disagree with RSO and Vega$ NSX. With two die, your chances are 8/9.

Compared to rolling one die, you chances must improve with two since you can now fall back on the second die if the first one rolls 1 or 2.

I wouldn't hop on a plane to Vegas just yet chief :tongue:

The two rolls are statistically uncorrelated, so the second roll does not necessarily "help" the first. It is like playing roulette. If you spin 10 times, and the first 9 times you land on red, your 10th spin does not mean there is a higher probably of landing on black. The odds of landing on red or black on the 10th spin, is EXACTLY the same as on the 1st spin.

 

[RSO 34]

I disagree with RSO and Vega$ NSX. With two dice, your chances are 8/9.

Compared to rolling one die, you chances must improve with two since you can now fall back on the second die if the first one rolls 1 or 2. Look at it this way:

Let's call the dice D1 and D2 and let's just look at D1 first. You have a 2/3 chance of success based only on D1. That means there's a 1/3 chance where you'll want to check D2, which itself has a 2/3 chance of success.

2/3 + 1/3 * 2/3 = 8/9

If you don't believe your chances improve with two dice, imagine rolling 3, 4, 100, 1000, or a million. You can see your chances of success approach 100%, but never reach it (there's always the chance that all million dice will roll either 1 or 2).

English Lit major, eh? :wink:

 

[naaman]

Yes, but you ONLY "lose" if your final roll fails. So if you are playing roullette, and you get multiple chances, and any ONE of those chances succeeds, the previous failures are ignored.

So your chance to "win" should improve, right?

 

[RSO 34]

So if you are playing roullette, and you get multiple chances, and any ONE of those chances succeeds, the previous failures are ignored.

Tell that to the casino as they are counting up all the chips you lost on the "previous ignored failures". The biggest sucker enticer at Roulette is that "tote board" that displays the previous spins causing the statistically ignorant to believe that there is a higher probability of a certain number to hit as a result of it not coming up for a while or, conversely, believing there is a lower probability of the same number coming up on consecutive spins.

 

[whatisreal7]

Let me ask you a questions: when you flip a coin, and expecting it to either be heads or tails, do you ask yourself what were the results of the previous times you've flipped the coin in your lifetime, and how it might affect this result? I hope your answer is no, because when you flip a coin now, there is, and always will be, a 50% chance of it landing on either side.

 

[whatisreal7]

RSO, sounds like you and I need to meet up with Naaman and Ojas for a nice game of poker =)

 

[naaman]

But that's not what I'm asking.

Suppose the bet is based on a coin toss. But you get to filp the coin twice, and your opponent must "pay" if EITHER coin toss comes up in your favor. It is two separate coin tosses, yes. But your opponent is giving you two chances to make the toss, and will pay your your dues if at least one of them comes up as you call it.

Do you see the difference between your original interpretation and this scenario?

 

[naaman]

RSO, sounds like you and I need to meet up with Naaman and Ojas for a nice game of poker =)

Okay, let me ask you this:

If you won a hand of poker but the conditions were that you had to beat me twice (but I only had to beat you once) to claim the pot, would you still want to play?

 

[RSO 34]

Let me ask you a questions: when you flip a coin, and expecting it to either be heads or tails, do you ask yourself what were the results of the previous times you've flipped the coin in your lifetime, and how it might affect this result?

Only Estragon and Vladimir would contest that hypothesis (I threw in this obscure literary reference for the statistically challenged mathletes who majored in English Lit).

 

[RSO 34]

Okay, let me ask you this:

If you won a hand of poker but the conditions were that you had to beat me twice (but I only had to beat you once) to claim the pot, would you still want to play?

If you had to put up double my bet, yes.

 

[Ojas]

The two rolls are statistically uncorrelated

Yes, I am aware of this and never claimed otherwise, which is why I wrote the following (I highlighted D1 and D2's probability of success in red and blue)...

You have a 2/3 chance of success based only on D1. That means there's a 1/3 chance where you'll want to check D2, which itself has a 2/3 chance of success.

2/3 + 1/3 * 2/3= 8/9

If you don't believe me, run a simulation in your programming language of choice. Some code like this would do the trick:

var iterations = 100000;
var successCount = 0;
for (var i=0; i<iterations; i++)
{
    var d1 = Math.floor(Math.random()*6)+1;
    var d2 = Math.floor(Math.random()*6)+1;
    var win = d1 >= 3 || d2 >= 3;
    if (win)
        successCount++;
}

var successRate = successCount/iterations;

Unfortunately, I don't know how to explain it any clearer. On the topic of Vegas and roulette, perhaps we should settle this with a friendly wager.

 

[Vega$ NSX]

The thing is odds are different than chances. Odds is a very simple math formula of winning outcomes divided by total number of outcomes. This is usually fixed: sides to a die, sides to a coin, card combinations etc. Chances are different than odds. If you flip a coin, you will always have a 50/50% odd of getting it right. No matter how many times you flip the odds will always remain 50%. Now it's a given that if you keep flipping that coin, you will eventually get it right, but it will always be at 50/50% odds.

In your case of roll again for free, you are only looking at it from a win only perspective, which is what I think may be throwing you off. In a flip again for free scenario where you can only win, of course each roll or flip of the coin will give you a benefit because the more opportunities will only mean more chances to win. If you keep rolling or flipping for free isn't it just an inevitability that you will win? Yes. This is the case if it is a 1% or 99% odds of winning. However, this is not a statistical benefit. You still have the same odds, but it never hurts to keep trying because you just get more chances. You just have more chances at the same odds. For example, if you win according to the odds, you have a 1 in 6 odd of getting a roll of a die right. You have a 1 in 2 odd of guessing a coin flip. If you flipped a coin twice you should have one win. If you rolled a die 6 times you should also have one win. Note that the odds never changed even though the total win tally is the same. That is because it took you 3 times as many rolls with the die to get the same number of wins as flipping the coin. That need for additional rolls, is reflected in the lower odds of the die to the coin. The odds just state that you will win sooner. If you flipped a coin or rolled a die, I would be willing to bet that you will guess right sooner with the coin than the die. That is because the odds are greater. 50% as opposed to 16.67%

Vegas casinos live and die by this concept. They often have odds in the single digit advantage, like 52/48%. However, each time a hand of blackjack is dealt the odds are they are going to win. Even if you said double or nothing, they still have the odds stacked in their favor. The more chances you get only proves out their odds.

 

[naaman]

Yes, I am aware of this and never claimed otherwise, which is why I wrote the following (I highlighted D1 and D2's probability of success in red and blue)...



If you don't believe me, run a simulation in your programming language of choice. Some code like this would do the trick:

var iterations = 100000;
var successCount = 0;
for (var i=0; i<iterations; i++)
{
    var d1 = Math.floor(Math.random()*6)+1;
    var d2 = Math.floor(Math.random()*6)+1;
    var win = d1 >= 3 || d2 >= 3;
    if (win)
        successCount++;
}

var successRate = successCount/iterations;

Unfortunately, I don't know how to explain it any clearer. On the topic of Vegas and roulette, perhaps we should settle this with a friendly wager.

Okay, so... If this is correct, that means that a free re-roll doesn't actually double your chances, rather it brings them up to (in this case) somewhere around 89%.

RSO: my question about the poker game was more to illustrate the likelihood of actually winning a pot when one player gets it if he wins at all, while the other player only gets it if he wins twice in a row (assume all hands are "showing" for the whole game). The player who must only win one game suffers no penalty (i.e betting double). He simply has an (unfair, in this case) advantage.

 

[Ojas]

Who wants to bet?

just count the W's

32/36 = 8/9 = 88.89%

 

[naaman]

Instead think of it this way. If I flip a coin and I am right, then you give me $10. If I am wrong I give you $10. Is there any statistical advantage for flipping again for free? Techically no becuase the odds will stay the same at 50/50%. Then if I skewed it so that if the odds were in my favor, say 75/25%, would you be at a statistical benefit to flip/roll again? No, you'd actually be a statistical disadvantage.

Okay, but what I want to know is this:

If we play the coin toss game and the rules are as follows, how do you calculate the advantage:

Naaman vs. Vega$ coin toss. In this game, Naaman will flip a coin. If it comes up heads, Vega$ will pay Naaman $10. If it comes up tails, Naaman will flip the coin again. If it comes up heads, Vega$ will pay Naaman $10. If it comes up tails a second time, Naaman will pay Vega$ $10.

How do you claculate that?

 

[naaman]

Re: Who wants to bet?

just count the W's

32/36 = 8/9 = 88.89%

I think this is exactly what I was trying to explain a couple posts up.

 

[RSO 34]

Re: Who wants to bet?

just count the W's

32/36 = 8/9 = 88.89%

That is where you are making your mistake. You are looking at the potential total number combinations which would be 6 squared (6 numbers, 2 dice) exceeding the potential combinations of 2, 3, 3 and 4. However, the initial hypothetical was based upon a single number between 3-6 and not the total of two dice. The hypothetical has only 12 potential outcomes based upon the probability of a single number on a single die hitting of which there is total of 8 chances. Your 88.89% chance reflects the odds of any combination of numbers totalling greater than 4 when two dice are thrown of which there are 32 out of 36 chances that the total of two thrown dice will be greater than 4.

Your calculations would come into play if the question asked the statistical probability of rolling five 1's with five dice:

There are 7776 possible results with 5 dice; 6^5 or 6*6*6*6*6. Only one of these throws will result in all ones so the odds are 1 in 7776. A side issue is what are the odds that you won't throw a 1 with 5 dice (or any other specific number). The answer is (5^5)/(6^5); 3125/7776 or 0.40188. This also indicates that you will throw at least one 1 4651/7776 times or 0.59812. (Almost 60 percent of the time you will throw at least one 1.)

 

[naaman]

RSO, I think this is starting to get onto the right track.

Suppose I rolled both dice together (all 12 sides). The only way NOT to succeed would be if BOTH dice simultaneously came up as a 1 or 2. Each die has an inidvidual 33.3% chance to land on 1 or 2. But both together landing on 1 or 2 is 1/3 *1/3 or 1/9, or roughly 11%. (my earlier post of this same problem is wrong: I said it would be 16.67%).