I swear! The things that go through my head when I'm bored....:redface:
Okay so here it is:
If there is a given likelyhood of something occuring, we can represent that with a percentage. Such as 30% likely.
Now, if the likelihood doubles, it should become 60% likely, right?
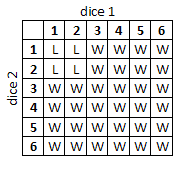
But, what if the likelihood doubled again? For example, you roll a die and you are looking for it to come up as a 3 or higher (66.67% chance). Now, if you roll two dice and need at least one (both are not necessary) to come up three or better, the likelihood is doubled, but what percentage is it that one or the other will come up three or better? It's obviously not 133%.
The only thing I could think of would be to cut the likelihood of failure in half. So for example, on a single die you have a 33.3% chance to fail, while the chances of both dice failing is only 16.67%. But then, that's not really "doubling" the chance for success, since by that method your chances for success are 83.3%, which is not twice as much as 66.67%.
Since the outcome of the first die has no impact on the outcome of the second die, the odds should be doubled, but I can't figure out how to represent that with a percentage.
So what is the answer? I'm stumped.
Okay so here it is:
If there is a given likelyhood of something occuring, we can represent that with a percentage. Such as 30% likely.
Now, if the likelihood doubles, it should become 60% likely, right?
But, what if the likelihood doubled again? For example, you roll a die and you are looking for it to come up as a 3 or higher (66.67% chance). Now, if you roll two dice and need at least one (both are not necessary) to come up three or better, the likelihood is doubled, but what percentage is it that one or the other will come up three or better? It's obviously not 133%.
The only thing I could think of would be to cut the likelihood of failure in half. So for example, on a single die you have a 33.3% chance to fail, while the chances of both dice failing is only 16.67%. But then, that's not really "doubling" the chance for success, since by that method your chances for success are 83.3%, which is not twice as much as 66.67%.
Since the outcome of the first die has no impact on the outcome of the second die, the odds should be doubled, but I can't figure out how to represent that with a percentage.
So what is the answer? I'm stumped.